In the realm of healthcare, education, and policy-making, understanding the effects of treatments and interventions is paramount. However, discerning causality from mere correlation can be challenging. In this blog post, I invite you on a journey to unravel the complexities of estimating the true impact of interventions. From exploring randomized controlled trials to delving into the intricacies of confounding variables, join me as we navigate through the fascinating world of causal inference and uncover the methods and insights essential for evidence-based decision-making.
Potential Outcomes Notation
To generalize our understanding, let’s introduce notation for the potential outcomes framework:
- \(Z\) denotes the treatment/exposure condition, where \(Z = 1\) represents treatment and \(Z = 0\) represents control.
- \(Y\) represents the observed outcome variable.
In this framework, we explore how observed \(Y\) values would vary with different treatments:
- For binary \(Z\), we denote potential outcomes as \(Y^1\) (under treatment, \(Z = 1\)) and \(Y^0\) (under control, \(Z = 0\)).
In reality, individuals are assigned to only one treatment group at a time, so we can’t know both potential outcomes for an individual simultaneously. We’ll address this later; for now, assume we know both \(Y^0\) and \(Y^1\) values.
If we had access to both potential outcomes for each individual, we could derive various statistics to assess treatment effects:
- Individual Treatment Effect (ITE): Calculated as \(Y^1 - Y^0\), directly comparing potential outcomes.
- Average Treatment Effect (ATE): Obtained by averaging all individual treatment effects, representing the difference between the averages of \(Y^1\) and \(Y^0\).
However, a crucial challenge arises: how do we compute ITE or the true ATE when we can’t observe the counterfactual outcome? This highlights the core issue of causal inference, which is essentially grappling with missing data. Since we only witness the actual outcome, the counterfactual remains elusive.
The following table displays data for 12 hospital patients who either interacted with a stress-relief toy (\(Z = 1\)) or did not interact with a stress-relief toy (\(Z = 0\)).
The theoretical data contains both potential outcomes, allowing us to compute the true ATE by subtracting the potential outcome averages. The true ATE is -5.8, indicating that interaction with stress-relief toys results in an average decrease in cortisol levels of 5.8 units.
| Z |
Y¹ |
Y° |
Y¹ - Y° |
| 1 |
18 |
23 |
-5 |
| 0 |
17 |
22 |
-5 |
| 1 |
15 |
23 |
-8 |
| 1 |
16 |
24 |
-8 |
| 0 |
17 |
23 |
-6 |
| 1 |
15 |
21 |
-6 |
| 0 |
9 |
14 |
-5 |
| 1 |
8 |
15 |
-7 |
| 1 |
10 |
14 |
-4 |
| 0 |
8 |
13 |
-5 |
| 0 |
8 |
14 |
-6 |
| 1 |
10 |
15 |
-5 |
| Average |
12.6 |
18.4 |
-5.8 |
Real data includes only one potential outcome per individual. Notably, \(Y^1\) values are absent for individuals in the control group (\(Z = 0\)), while \(Y^0\) values are absent for those in the treatment group (\(Z = 1\)). Consequently, in practical scenarios, we consistently lack half of the necessary data to compute the true ATE.
| Z |
Y¹ |
Y° |
Y¹ - Y° |
| 1 |
18 |
? |
? |
| 0 |
? |
22 |
? |
| 0 |
? |
23 |
? |
| 1 |
16 |
? |
? |
| 0 |
? |
23 |
? |
| 1 |
15 |
? |
? |
| 0 |
? |
14 |
? |
| 1 |
8 |
? |
? |
| 1 |
10 |
? |
? |
| 0 |
? |
13 |
? |
| 0 |
? |
14 |
? |
| 1 |
10 |
? |
? |
| Average |
? |
? |
? |
Estimating the ATE
To estimate causal effects without knowing both potential outcomes for individuals, we rely on randomization, a method of treatment assignment akin to a coin flip. This ensures similarity between treatment groups, except for the treatment itself. While we can’t observe individual counterfactual outcomes, we can reasonably assume similar individuals received each treatment, allowing us to estimate unobserved potential outcomes.
With randomization, we estimate the ATE by comparing average observed outcomes between treatment and control groups. In our example, the estimated ATE is -5.4, closely aligning with the true ATE of -5.8 calculated earlier.
Average \(Y\) for \(Z = 1\): (18 + 16 + 15 + 8 + 10 + 10) / 6 = 12.8
Average \(Y\) for \(Z = 0\): (22 + 23 + 23 + 14 + 13 + 14) / 6 = 18.2
Estimated ATE from Randomized Treatment: 12.8 - 18.2 = -5.4
Confounders and Selection Bias
When randomization isn’t feasible due to ethical or practical reasons, bias can affect causal effect estimates. Selection bias is a primary concern, occurring when individuals are assigned to treatment or control groups non-randomly.
In our stress-relief toy example, selection bias may occur if:
- Individuals self-select for therapy.
- Control group individuals originate from a different hospital.
- Access to therapy is tied to external factors like insurance.
Variables associated with treatment assignment that also affect the outcome (cortisol level) are confounders. These can lead to erroneous conclusions about treatment impact.
Estimating the ATE with Confounders
To estimate the ATE in the presence of confounders, we must address how treatment assignment impacts outcomes when randomization isn’t feasible. Consider our stress-relief example:
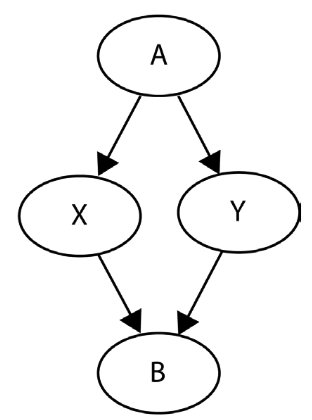
Instead of random assignment, let’s imagine patients can choose therapy. Additionally, we have data on a new confounding variable \(X\) indicating anxiety diagnosis (\(X = 1\)) or absence (\(X = 0\)). Anxiety status influences treatment choice and cortisol levels: those with anxiety may opt for therapy and have higher cortisol levels.
This scenario poses a problem as it could lead to an imbalance in anxiety levels between treatment groups. Conditional exchangeability is crucial here:
- Conditional exchangeability ensures treatment groups are comparable when considering confounding variables.
- This concept, also known as ignorability or unconfoundedness, prevents biased estimates.
By accounting for anxiety diagnosis (variable \(X\)), we avoid biased cortisol level estimates between therapy-receiving and non-receiving groups.
For example, the following table includes data for twelve hospital patients who self-selected therapy toys. Variables include anxiety diagnosis (\(X=1\) for anxiety, \(X=0\) for no anxiety) and treatment assignment (\(Z=1\) for therapy, \(Z=0\) for no therapy). As this reflects reality, only the observed outcome \(Y\) (cortisol level) is available.
Without considering anxiety (\(X\)), computing the estimated ATE as if treatment were randomized yields -2.9. This suggests therapy toys services reduce cortisol levels by an average of 2.9 units.
| X |
Z |
Y |
| 1 |
1 |
18 |
| 1 |
1 |
17 |
| 1 |
1 |
15 |
| 1 |
1 |
16 |
| 1 |
0 |
23 |
| 1 |
0 |
21 |
| 0 |
1 |
9 |
| 0 |
1 |
8 |
| 0 |
0 |
14 |
| 0 |
0 |
13 |
| 0 |
0 |
14 |
| 0 |
0 |
15 |
Average \(Y\) for \(Z=1\): (18+17+15+16+9+8)/6 = 13.8
Average \(Y\) for \(Z=0\): (23+21+14+13+14+15)/6 = 16.7
Estimated ATE: 13.8 - 16.7 = -2.9
To address the anxiety variable, we compute the ATE specifically for patients diagnosed with anxiety disorder (\(X=1\)). By subtracting the average cortisol level for control patients from the treated group, we aim to ensure similar cortisol levels before therapy. This yields an estimated ATE of -5.5 for individuals with anxiety, significantly higher than the initial estimate of -2.9.
| X |
Z |
Y |
| 1 |
1 |
18 |
| 1 |
1 |
17 |
| 1 |
1 |
15 |
| 1 |
1 |
16 |
| 1 |
0 |
23 |
| 1 |
0 |
21 |
Average \(Y\) for \(Z=1\): (18+17+15+16)/4 = 16.5
Average \(Y\) for \(Z=0\): (23+21)/2= 22.0
Estimated ATE for \(X=1\): 16.5 - 22.0 = -5.5
Next, we calculate the ATE specifically for patients without an anxiety disorder diagnosis (\(X=0\)). The estimated ATE for individuals without anxiety is also -5.5.
| X |
Z |
Y |
| 0 |
1 |
9 |
| 0 |
1 |
8 |
| 0 |
0 |
14 |
| 0 |
0 |
13 |
| 0 |
0 |
14 |
| 0 |
0 |
15 |
Average \(Y\) for \(Z=1\): (9+8)/2 = 8.5
Average \(Y\) for \(Z=0\): (14+13+14+15)/4 = 14.0
Estimated ATE for \(X=0\): 8.5 - 14.0 = -5.5
When considering \(X\), averaging the ATEs of both groups yields an estimated ATE of -5.5. This is closer to the true ATE of -5.8, indicating that therapy animal services reduce cortisol levels by an average of 5.8 units. Accounting for confounding significantly improved our estimate’s accuracy.
| ATE Estimate |
Value |
| Ignoring X |
-2.9 |
| Accounting for X |
-5.5 |
| True Value |
-5.8 |
]]>